Singapore Synchrotron Light Source

Makes Light Work For You
  • Home
  • XDD: X-ray Reflectometry and Diffractometry

  • XDD: X-ray Reflectometry and Diffractometry

    Contact: Dr. Yang Ping (slsyangpnus.edu.sg)

  • Introduction


    Methods:
    • High-resolution X-ray diffractometry (HR-XRD)
    • X-ray Reflectometry (XRR):nano-measurement to determine density, thickness and roughness of a film
    • Powder Diffractometry
    • X-ray Diffraction Topography

    Introduction


    Applications:
    • High-resolution X-ray diffractometry (HR-XRD)
    • X-ray Reflectometry (XRR):nano-measurement to determine density, thickness and roughness of a film
    • Powder Diffractometry
    • X-ray Diffraction Topography

  • Applications:

  • XDD beam line and its experimental station are designed for a general purpose of diffractometry, fluorescence detection and absorption spectroscopy, which will serve the research and development with structural determination, characterization and process monitoring in universities, institutes and industry in Singapore and the region. Following applications are proposed:
    • High-resolution diffraction (HR-XRD): to determine precisely structure parameter, minute strain status, composition, thickness, surface/interface roughness and texture/stress analysis;
    • Grazing-incidence X-ray diffraction (GI-XRD), X-ray reflectometry (XRR) and diffuse scattering: to determine surface and interface structure /ordering, surface phase identification/transition, layer thickness and density;
    • Powder diffraction: structure determination and refinement, phase identification in quality and quantity, lattice-parameter determination, crystal grain size & texture/stress analysis;
    • Fluorescence: element analysis, X-ray standing wave;
    • Absorption spectroscopy: XAFS (X-ray absorption fine structure);
    • X-ray diffraction topography.

    Spectrum (phs/s/mradH/500mA/0.1%BW) of Helios 2:
    Source parameters (port 1): δx=1.45 mm, δy=0.33 mm, δx’=1.49 mrad, δy’=0.16 mrad, 2.3–10 keV available.
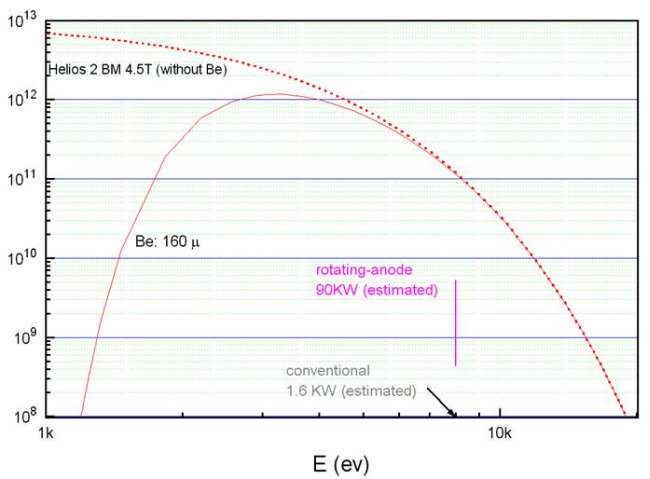    Fig. 1. Radiating spectrum from the Helios 2 and absorbed spectrum for XDD beamline, Beryllium thickness 160 μm in the end-window of the beamline. The flux density at 8.048 keV is about 20 times of that from a rotating-anode 90KW X-ray generator and about 1000 time of a conventional 1.6 KW X-ray generator.
  • Beamline layout:
  • Diffractometer:
    Huber 4-circle system 90000-0216/0 diffractometer is shown in Fig. 3 and its specification is listed in Table 1.
    Fig. 3. Huber 4-circle system 90000-0216/0 with a Si (111) analyzer in XDD beamline. Four circles 2θ, ω, χ and φ, X,Y, and Z-table, slit system are shown.
  • Table 1. Specification of the goniometer
    Range Precision (step-size) Repeatability
    ω 0-360° (without accessory) 0.0001° +/-0.0005°
    2θ 0-360° (without accessory) 0.0001° +/-0.0005°
    χ -3-+93°(1/4 circle Eulerian cradle) 0.0001° +/-0.001°
    φ 0-360° 0.0005° +/-0.0005°
    X,Y table 0-150 mm 0.001 mm +/-0.001 mm
    Z-table 0-10 mm 0.001 mm +/-0.001 mm
  • Attachments: X-ray fluorescence detecting system: XR-100R Si diode detector and MCA8000A multi-channel analyzer, AMPTEK Inc. Energy resolution: 215 eV@5.9 keV. Absorption spectrum measure system: ion-chambers attached to the diffractometer.
    Ref: 1. HIGH-RESOLUTION X-RAY DIFFRACTOMETRY AT SINGAPORE SYNCHROTRON LIGHT SOURCE, P. Yang and H.O. Moser, SSLS internal manuscript. 2. High Resolution Reflectometry at Singapore Synchrotron Light Source, P. Yang and H.O. Moser, Advances in Synchrotron Radiation, Vol. 1, No. 1 (2008) 105–113, World Scientific Publishing Company.

  • High-resolution X-ray diffractometry: (HR-XRD) *

  • HR-XRD is a kind of diffractometry technique to measure diffraction peaks (heights, positions and profiles) precisely with small-angular-divergence of incident X-ray beam, high-precision of goniometer, and small-angular-acceptance of detection system. It is widely used in research, development, and manufacture for characterization of epi-layer growth, quality control and determination of structure parameters. As shown in Fig. 4, HR-XRD can offer epi-layer orientation, precise structure parameter, composition, thickness, surface/interface roughness and minute strain/stress status and texture.
    Fig. 4. Film status can be revealed by HR-XRD (reprinted from: D. Keith Bowen and Brian K. Tanner, High resolution X-ray diffractometry and topography, Taylor & Francis, London, Bristol, 1998).
    Experimental methods:
    1. Typical experiment condition of XDD:
      Helios 2: 700 MeV, typical 300 mA, CuKα1 radiation equivalent (8.048 keV in photon energy) by a Si (111) channel-cut monochromator (CCM),
      Incident beam size: 1.0 mm x 3.5 mm, by slits,
      Incident beam photons: 2x109 phs/s,
      Incident beam divergence: about 0.006°.
    2. Powder diffractometry
      As a comparison, scheme of diffraction geometry for a polycrystalline sample is as shown in Fig. 5, known as powder diffractometry. If the divergences in the beams turn out to be very narrow close to a plane wave (shown as red lines), it becomes a high-resolution X-ray diffractometry.

    Fig. 5. Powder diffractometry (Bragg-Brentano geometry): advantage of auto-focusing for diffracted beam to collect more diffracted photons from poly-crystalline grains; Dis-advantage: rocking scan is broadened due to divergent incident beam and angular resolution is lower. k1 and k2 are centered wave vectors for incident and diffracted X-ray beam respectively. DS: divergence slit, Δα denotes the divergence in incident beam and RS: receiving slit, Δ2ϑ the divergence in diffracted beam. α is the incident angle and β the out-going diffraction angle against sample surface, 2θ≡α+β. q = k2 -k1 is a scattering vector.

    3) HR-XRD
    Schemes of diffraction geometry in HR-XRD for a single crystalline sample are as shown in Fig. 6 and Fig. 7. Basic angular scans can be performed according to corresponding circles’ motion as follows: • 2θ/ω coupled-scan: 2θ:ω increment ratio 2:1 • 2θ-scan: detector moves alone or using area-detector • ω -scan: rocking scan, ω moves alone • ϕ –scan: ϕ moves alone, not shown • χ –scan: χ moves alone, not shown • 2θ/ω off-set scan: not shown. An angle Δ2θ is always off-set in 2θ to the 2:1 position of 2θ/ω coupled-scan.
    Fig. 6. Diffraction geometry of HR-XRD, different angular scans are shown for a single crystalline sample. Such scans are along different direction in q-space. k1 and k2 are wave vectors for incident and diffracted X-ray beam respectively, with small-angular-divergences in it. α is the incident angle and β the out-going diffraction angle against sample surface, 2θ≡α+β. q = k2 -k1 is a scattering vector. Above scan modes are expressed with diffractometer angular coordinates (2θ, ω, χ, ϕ): 2θ≡α+β and ω≡α as described in Fig. 6. Such scans are along different direction in q-space. Generally, qx is in-plane and qz along the normal direction of sample. Scattering vector q(qx, qy, qz) are expressed by

    in crystal (reciprocal) coordinate system and can be deduced from the angular coordinates 2θ, ω, χ and ϕ that

    where χ=±90° and ϕ=0 (ϕ fixed mode), k = 1/ λ (no 2π), 2θ≡α+β as defined in Fig. 6, Г: angle between (00L) and (H0L) as in Fig. 7. θ is half of 2θ. If 2θ and ω0 are angles at a specular reflection for the Bragg planes, then Δω is the orientation difference or rocking rotation angle apart from this specular reflection condition ω0 that Δω =ω- ω0. In Bragg condition, 2θ and ω0 are denoted as 2θB and ωB respectively.

    Fig. 7. More general of diffraction geometry in HR-XRD for a (H0L) Bragg plane. Suppose that (00L) is along the normal of sample surface and Г is an angle between (00L) and (H0L) planes. k1 and k2 are wave vectors for incident and diffracted X-ray beam respectively. α is the incident angle and β the out-going diffraction angle against sample surface, 2θ≡α+β. q = k2 -k1 is a scattering vector.
    4) Reciprocal Space Mapping (RSM)
    RSM is a diffraction intensity distribution (as a weight) around a reciprocal space point (vector). It can reveal info of orientation and crystalline d-spacing in the sample. For a single crystalline sample in Fig. 6 or Fig. 7, if detector arm (2θ) is fixed at a series of angles and ω-scan is performed relative to its corresponding specular angles ω0 , such 2D diffraction intensity data form a 2θ–ω mapping, so-called reciprocal space mapping (RSM). Such mapping can be formed either by different scans shown above. The coordinates of such 2θ –ω mapping can be converted to q space coordinates (qx, qy, qz) using above formulae. Fig. 8 shows schematically an RSM in both of q space coordinate system (qx, qy, qz) and diffractometer angular coordinate system. In the mapping:
    Angular coordinates of mapping: Δ2θ & Δω
    Substrate peak: 2θB & ωB
    A centre along Δω: 2θ, ω0
    Δ2θ=2θ-2θB, ω0=Δ2θ/2+ ωB
    Δω=ω-ω0, θ =2θ/2
    Γ: angle between (00L) and (H0L).
    q-space coordinates (qx, qy, qz) are equally used.
    From (qx, qy, qz), a representation using Miller indices can be derived. For orthorhombic system, they are expressed as

    where a*, b* and c* are the basis in reciprocal space.

    Fig. 8. Schematic of an RSM in both of q space coordinate system (qx, qy, qz) and diffractometer angular coordinate system. In the mapping, dash-lined g is a reciprocal space vector, corresponding to the Bragg plane (H0L). Film and substrate diffraction peaks (spots) are shown in yellow and red respectively. Δ2θ and Δω are angles from the reference centre of 2θ (here substrate) and centres of ω0 respectively. (qx, qz) coordinate system is as shown either, in which the reciprocal space vector g is decomposed into qx and qz components, i.e., H and L respectively. 5) Reciprocal Space Vector (RSV) method: to determine the lattice parameters. RSV can be represented as

    • X-ray Reflectometry (XRR)

    • XRR offers surface and interface roughness, density/porosity, thickness of films as shown in Fig. 21.

      Some examples of XRR are as below:
      Fig. 22. SiGe on Si. The roughness, density and thickness obtained from XRR are compared with those obtained by AFM, SIMS and TEM. They are very close.
      Fig. 23. ZnS-SiO2/Ge2Sb2Te5/ZnS-SiO2 sandwich structures. Inter-diffusion, density and thickness changes have been obtained from XRR for different annealing temperatures.
      Fig. 24. Porous Polyaniline (PANI) layer. The data (inset) below the critical angle of Au confirm the existence of the double polymer layers.
      Fig. 25. A rocking scan shows diffuse scattering from a TiN film. Yoneda peaks are remarkably seen, whereas the reflection peak (at centre) is much weaker.
      Ref.: High Resolution Reflectometry at Singapore Synchrotron Light Source, P. Yang and H.O. Moser, Advances in Synchrotron Radiation, Vol. 1, No. 1 (2008) 105–113, World Scientific Publishing Company.

    • Powder diffractometry

    • With structure determination & refinement by powder diffractometry, it can offer crystal structure, phase identification in quality and quantity, lattice-parameters, crystal grain size & texture/stress.

      Fig. 26. Left) Principle of powder diffractometry (top); an example of structure determination & refinement by Rietveld analysis for (Bi3.19Nd2.81)Ti12O48 (middle) and anomalous scattering for La10-xNax(SiO4)6O3-x (lower). Up) diffraction patterns for a standard quartz sample.

    • X-ray topography

    • Scheme of X-ray topography is as shown in Fig. 27. It reveals long-range strain fields, inclusions, and various structural defects (point defect, dislocation, stacking fault, twin and angle boundaries).

      Fig. 27. Upper) Principle of X-ray topography. Transmission geometry (red line) and reflection geometry (blue line). Middle) Voids in a Si wafer. Lower) Surface stripes in PZN-PT single crystal.

      Monograph & References
      1. Ullrich Pietsch, Vaclav Holy, Tilo Baumbach，High Resolution X-ray Scattering: From Thin Films to Lateral Nanostructures，2nd Ed., Springer Science & Business Media, 2004, Springer-Verlag, New York LLC.
      2. D. K. Bowen, B. K. Tanner, High Resolution X-Ray Diffractometry and Topography，1st Ed., Taylor and Francis, 1998, London. DOI: https://doi.org/10.1201/b12575, eBook ISBN9780429224836.
      3. 麦振洪等著,《薄膜结构X射线表征》(第二版), 科学出版社, 2015.4., 北京.